Calculadora de triángulos isósceles calcula todas las propiedades de un triángulo isósceles tales como área, perímetro y lados, si se proporciona un subgrupo de éstas propiedades El triángulo isósceles es un polígono con tres vértices (esquinas) yTrigonometría y Triángulos Rectángulos Objetivos de Aprendizaje Usar el Teorema de Pitágoras para encontrar las longitudes desconocidas de los lados de un triángulo rectángulo Encontrar las longitudes y ángulos desconocidos de un triángulo rectángulo Encontrar los valores exactos de una función trigonométrica para ángulos que miden 30°, 45°, y 60°15 Un solar tiene forma de triángulo y se conocen dos lados,que miden 18 m y 23 m,y el ángulo que forman,que es de 125° El m2 vale 30 € Calcula el valor del solar Solución 1 —75= — sen A sen 65° 5 Tercer y cuarto casos de resolución de triángulos a = 8,4 m b = 7,6 m

Triangulo Entero Wikipedia La Enciclopedia Libre
Triangulo de 15 y 75 altura
Triangulo de 15 y 75 altura-Base y altura de triángulosEl carretillu La base de un triángulo es cualquiera de sus lados La altura es el segmento perpendicular desde una base al vértice opuesto de la misma Haciendo un clic en la imagen podrás ver todas las alturas que se pueden obtener en los triángulosConsideremos el ejemplo de dos árboles y sus sombras Supongamos que el sol brilla sobre los árboles, uno que mide 6 pies de alto y el otro con altura desconocida Al medir la longitud de cada sombra en el suelo, puedes usar la similaridad de los triángulos para encontrar la altura desconocida del segundo árbol




Triangulos Notables Ejercicios Resueltos Pdf
Resolución de triángulos 25 4UNIDAD 10 Página 113 1 En un triángulo ABC conocemos A ^ = 68°, b = 172 m y a = 1 m Calcula la longitud del lado c = 172 cos 68° = 64,43 m = 172 sen 68° = 159,48 m = = ,75 m c = = 64,43 m ,75 m = 154,18 m 2 En un triángulo MNP conocemos M ^ = 32°, N ^ = 43° y = 47 m8 Soluciones a los ejercicios y problemas 4 Calcula el lado desconocido en cada triángulo Lado A = 25 m Lado B = 63 mm 5 Calcula el lado desconocido en cada triángulo aproximando hasta las dé cimas Lado A = 12 cm › 17 cm Lado B = m › 5,7 m Lado C = mm › 15,5 mm 6 Tomando como unidad el lado del cuadradito, calcula el perímetro de la figura morada 3 6 cuadritosEl área se obtiene calculando (lado*altura)/2 para cualquier lado y su altura correspondiente Los lados y ángulos se obtiene usando el seno y coseno Se aplica las siguientes fórmulas a/sen(alpha)=b/sen(beta) (teorema de los senos) También se aplica para tres lados a,b,c y ángulo alpha opuesto a a a^2=b^2c^22bc cos alpha
ín notable de 15° y 75° a(Í6 TRIANGULOS RECTANGULOS NOTABLES APROXI MADOS t\ notable de 37° y 53° tx notable de 5372 = 26°30' notable de 3772 = 18°30' t\ notable de 16° y 74° 2 4 k fck notable de 8° y ° ^\5kV2~Respuesta (1 de 5) A Maria, Maria asumo que el área del cuadrado es de 25 cm², puesto que los cm no son una unidad de área, sino de longitud Los cuatro lados de un cuadrado son iguales, y puedes calcular uno de ellos (L) conocida el área A del cuadrado, como L En el triángulo isósceles de base BC, los ángulos que se oponen a los lados congruentes miden cada uno 15°, en consecuencia el triángulo rectángulo ABC,
Razones trigonométricas del ángulo mitad https//wwwyoutubecom/watch?v=0rO_CmcLgTransformando un radical doble a una suma de radicales simples https//wwHOLA COMO PUEDO SACAR EL AREA DE UN TRIANGULO EQUILATERO QUE ,MIDE X CM DE LADO Y UNA ALTURA DE Y CM Responder gerald necesito ayuda en hallar la altura de un triangulo equilatero que mide por lado 12cm Responder Julissa CedeñoCalcula la altura del pedestal tg 15° = 8 y = tg 55° = 8 y = E^= 180° – (A^ B^) = 75° Aplicando el teorema de los senos = 8 a = = 6,65 km dista de B = 8 b = = 9,38 km dista de A 31 En un entrenamiento de fútbol se coloca el balón en un punto situado a 5 m




Tengo Q Sacar Area De Eso Ayuda Xfa Brainly Lat




Geometria 21 V Ciclo Calameo Downloader
Razones trigonométricas de los ángulos de 75° y 15° 6 2 sen15 cos75 4 tan15 2 3 cot75 sec15 6 2 csc15 3 ÁREA DE UNA REGIÓN TRIANGULAR 31 Área en función de dos lados y el ángulo comprendido Determinando una altura del triángulo ABC Si h senC b , entonces h bsenC luego, absenC S 2 es el área de la región triangular ABC 32 ÁreaTenemos un triángulo rectángulo con alturltura=1666 y te piden construir un triángulo con 54m de alturaCuadrada de tres Este triángulo origina al triángulo notable de 15° y 75° Triángulo de 15° y 75° La altura relativa a la hipotenusa mide la cuarta parte de la longitudde dicha hipotenusa Triángulo de 36° y 54° Este triángulo origina al triángulo notable de 18° y 72°




コンプリート 15 Y 75 Triangulo Notable 1067 Triangulo Rectangulo Notable De 15 Y 75 Josspix8pyh




La Formula De Heron Para El Area De Un Triangulo Y Resolver Problemas Con Trigonometria Ck 12 Foundation
Lo bueno, malo y feo de la capacitación a directores Jesus Mendez Leer Teoría Triángulo Notable de 15° y 75° previous Razones trigonométricas de ángulos notables Parte II next Triángulo Notable de 37°/2 y 53°/2 Jesus MendezRespuestamide 75 cmExplicación paso a pasola área de un triángulo es base por altura dividido entre dos10x15 = 75 2 antonelad1907 antonelad1907 BC es el cateto opuesto y altura de la cometa (y) AC es la hipotenusa (h1) y coincide con la longitud de la cuerda L1= 80 m El ángulo a= 30º es el formado por los lados AB y AC Por tanto, sen a= y/h1 sen 30º= y/80 1/2= y/80 y= 80/2= 40 m de altura Con la 2º cometa se forma el triángulo rectángulo DBC DB es el cateto contiguo




Triangulo Notable De 15 Y 75 6 Youtube




Grupo Uni Ingreso Seguro Material De Geometria Hoy Miercoles 25 De Agosto A Partir De Las 10 30pm Transmision De Geometria Construcciones Y Trazos Auxiliares En El Triangulo Docente Manuel Trujillo
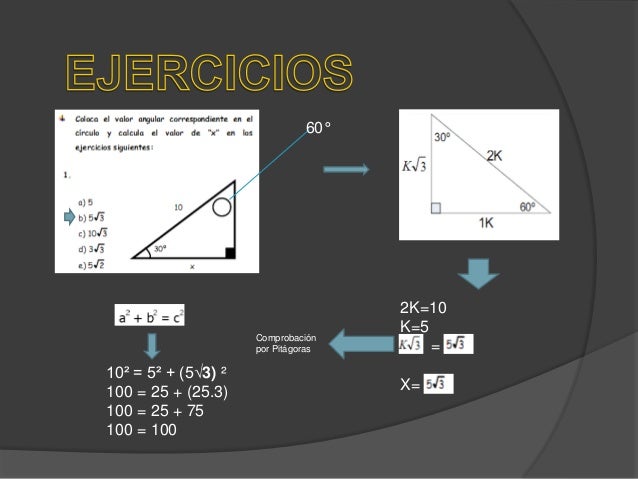
El área de un triángulo es base ( b b) por altura ( a a) divido entre 2 Como sabemos que el área es 15 c m 2 15 c m 2 y que la base es b = 6 c m b = 6 c m, podemos calcular la altura La altura del triángulo es 5cm Finalmente, calculamos la hipotenusa aplicando Pitágoras La hipotenusa mide, aproximadamente, 781cm FuentesAl conocer el area y la medida de su base procedemos a utilizar la formula del triángulo A=bh/2 área = 75 base = 2/3 h entonces reemplazamos A=bh/2 75= 2/3 h h /2 pasamos a multiplicar el 2 y nos queda 150= 2/3 h h aqui multiplicamos las "h" 150= 2/3 h 2 procedemos a pasar el 3 a multiplicar 450= 2 h 2 y el 2 pasa a dividir 450/2 = h 2 7 Triangulo Notable De 30 Y 60 Y De 45 Triangulos Rectangulos Notables Ejercicio Triángulos rectángulos notables ejercicio resuelto triangulo notable de 30° y 60° , y de 45°recomiendo ver estas listas de reproducciÓn del profe rodolfo Como resolver un ejercicio de triangulos rectangulos no doovi triángulo notable de 30° y 60




Triangulos Notables Ejercicios Resueltos Pdf



Cual Es El Valor Del Perimetro De Un Triangulo Gauthmath
Solución Paso 1 decide cuál razón trigonométrica usar Enfoquémonos en el ángulo , pues es el que está dado explícitamente en el diagrama Observa que nos han dado la longitud de la , y nos piden determinar la longitud del lado al ángulo La razón trigonométrica que utiliza a estos dos lados es el seno Triangulo de 15 y 75 grados Triángulo notable de 37/2 grados Triángulo notable de 53/2 grados Los triángulos notables más usados Los triángulos notables más importantes, por así decirlo, son aquellos que se ven con mayor frecuencia en soluciones de problemas en materias como la geometría, trigonometría, física y otrosDOY CORONITA C triangulo notable de




Tangente Triangle




Guia Adicional De Matematica 13 By C E T A E T I Issuu
Esto puede hacerse en un solo paso por lo cual la fórmula quedará Por ejemplo calcularemos el volumen del cilindro que tiene 14cm de radio y cm de altura V = 3,14 (14cm) 2 cm = 3,14 196cm 2 cm = ,8cm 3 Verás que primero se resuelve la potenciación (14cm x 14cm) y luego se multiplica por los otros dos númerosTriángulos elementos de un triángulo (vértices, lados, angulos interiores, exteriores, alturas, bases, medianas, bisectrices, ortocentro, baricentro, incentro) y clasificación según los ángulos (rectángulos, oblicuángulos, obtusángulos, acutángulos) y según los lados (equilátero, isósceles y escaleno) Test en línea sobre los conceptos y ejerciciosUno de los elementos más importantes de un triángulo es su altura Más propiamente, deberíamos decir "sus alturas", en plural, puesto que un triángulo tiene tres alturas En efecto, la altura es la menor distancia entre un vértice y el lado opuesto (o su prolongación), por lo que a cada vértice le corresponde una altura




1 4 Proporcionalidad De Perimetros Areas Y Volumenes En Objetos Semejantes Si Dos Figuras Son Semejantes Entonces Se Verifica Que V 3 Pdf Free Download




Trigonometria Preuniversitaria Cuarta Guia Resuelta Preguntas Tipo Examen De Admision A La Universidad
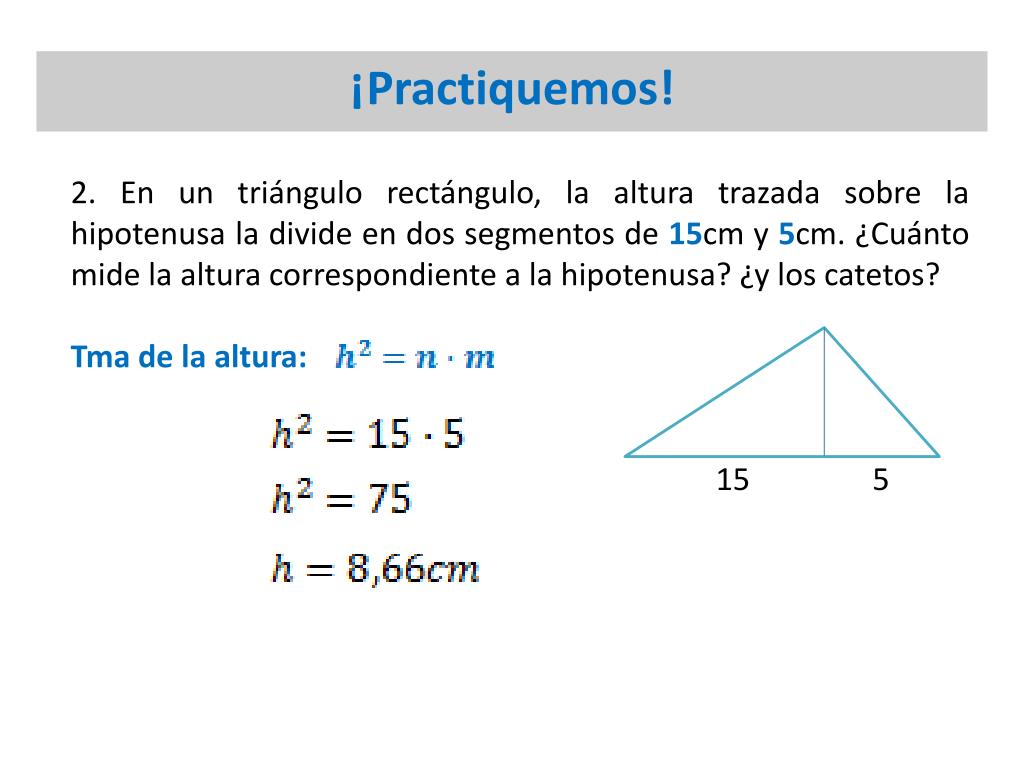
A) 60°, 80° y 100° b) 40°, 60° y 80° c) 30°, 40° y 50° d) 45°, 60° y 75° e) 36°, 48° y 60° 22 Calcule la medida del ángulo formado por la altura y la bisectriz que parten del vértice A de un triángulo ABC Sabiendo que m ) A 2(m ) C) = 100° a) ° b) 30° c) 40° d) 50° e) 60° 23 Los catetos de un triángulo rectángulo ABC miden AB = 8 u;A) El ángulo complementario de 15° es 75° y el suplementario es 165° b) El ángulo complementario de 47° es 43° y el suplementario es 133° c) El ángulo complementario de 78° es 12° y el suplementario es 102° d) El ángulo complementario de ° es 1° y el suplementario es 91° Estos triángulos son semejantesTeorema de la altura y de los catetos de un triángulo rectángulo Sea el triángulo rectángulo ∆ ABC , ºAˆ =90 Sea la altura h =AH sobre la hipotenusa Sea m =BH la proyección del catetos c sobre la hipotenusa Sea n =HC la proyección del catetos b sobre la hipotenusa Entonces, a) nh2 =m⋅ Teorema de la altura




Mathebox Tema Relaciones Metricas En El Triangulo Facebook




Triangulos 5to Ano Ejercicios Pdf Geometria Triangular Triangulo
Si en un triángulo rectángulo conocemos el ángulo de elevación y la base, podemos calcular la altura de triángulo con la relación A) Tangente B) seno C) cosecante D) Si en un triangulo rectángulo la base y altura tienen el mismo valor, entonces la tangente vale;De la I ^ hipotenusa o longitud de un cateto = ( longitud de 1 cateto ) xDescubre qué es un triángulo isósceles, cómo calcular el perímetro, altura y área de un triángulo isósceles Un triángulo isósceles es un polígono de tres lados, en donde, dos lados son de igual medida(a), por lo tanto, se tiene dos ángulos iguales (α) y otro diferente (β)
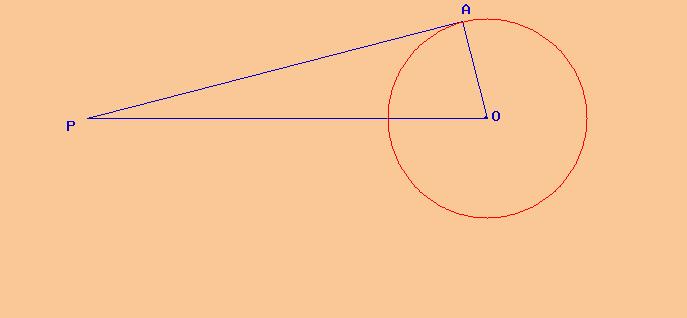



Solucionador Automatico De Problemas De Geometria El Triangulo




Semejanza De Triangulos Pdf
hola quisiera saber la altura de mi triangulo de 90° área 735 y base 4 Escribir cuanto es la altura de la pared y la distancia entre la pared y la˗ Altura de la rampa 1,5 metros triángulo notable de 15 y 75° Relaciono las longitudes de los lados de ambos triángulos En 2, calculo el valor de la constante k Calculo la longitud x de la rampa x = 4k x = 4(1,44 m) x = 5,76 m 1,5 m = k( 6– 2)A) Las dimensiones de una torre cilíndrica que en la maqueta mide 6 cm de altura y 4 cm de diámetro b)La superficie de un jardín que en la maqueta ocupa 40 cm2 c) El volumen de una piscina que en la maqueta contiene cm3 de agua a) La torre cilíndrica mide 15 m de altura y 10 m de diámetro b)40 250 2= cm = 250 m2




コンプリート 15 Y 75 Triangulo Notable 1067 Triangulo Rectangulo Notable De 15 Y 75 Josspix8pyh




Ejercicios Con Triangulos Oblicuangulos Superprof
Jugando un poco con las opciones mediante una hoja de cálculo y un poco de trigonometría, encontré éstas si un triángulo equilátero mide 7 unidades de lado, su altura medirá muy poco más de 6 De la misma forma, si la base es 8, la altura será casi 7 y si la base es 15 la altura será prácticamente 13 Pueden hacer la pruebaA) 24 B) 2 C) 25,15 B) 2 C) ,56 D) 15² = a² 7,5² agrupando valores a² = 15² 7,5² = 225 56,25 = 168,75 calculando a a = √168,75 = 12,99 cm o 13 por redondeo la altura del triángulo área = (b * h) / 2 sustituyendo por los valores conocidos área = (15 * 13) / 2 = 97,5 cm ² A 1jaiz4 y otros 37 usuarios les ha parecido útil esta respuesta



Ppt Recordemos Por Que Estamos Aqui Recordais El Dia Que Me Subi Encima De La Silla Powerpoint Presentation Id




Matematicas Resueltos Soluciones Triangulos Rectangulos Nivel I 1º Bachillerato Pdf Triangulo Funciones Trigonometricas
En general, un triángulo es una figura geométrica de tres lados Éstos pueden ser representarlos con una letra mayúscula, los ángulos con una letra minúscula y los vértices con las mismas letras anteriores o con letras griegas Para calcular su área, podemos utilizar la fórmula A = ½ (Base Altura) Sin embargo, existen otrosLa altura de un triángulo es el segmento de recta que se traza perpendicularmente (90°) desde un vértice hacía el lado opuesto de éste Vea la siguiente figura El segmento BH es la altura de este triángulo A la altura también se le conoce cómo la «distancia mínima» de un vértice hacía su lado opuesto Al punto «H» (donde cae laConociendo la altura, calculamos el área (15√3 30)/2 = 225√3 ¡Un saludo!




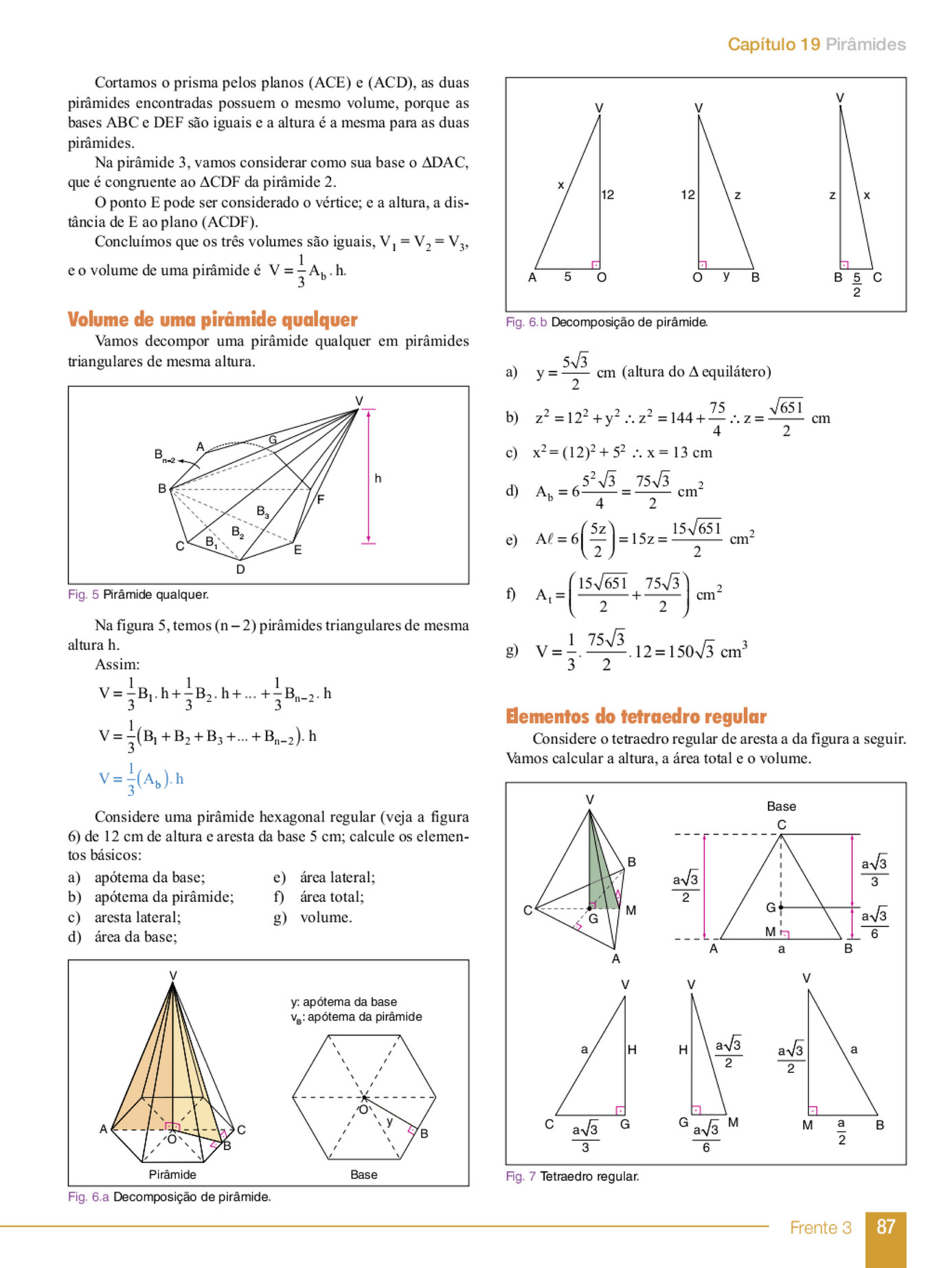



My Publications Matematica 4 Pagina 86 87 Created With Publitas Com
Altura _____cm Volumen _____ 2El volumen de un cono es de 96 y tiene una altura de 8 Calcula el diámetro de la base Diámetro de la base _____ 3Una pila de arena en forma de cono mide 2m de altura y su perímetro es de 14mDe un triángulo rectángulo ABC se conoce la hipotenusa, que mide 15 centímetros, y uno de sus ángulos,, que mide Resuelve el triángulo Puesto que es un triángulo rectángulo, habrá un ángulo de 90 y se puede calcular el que falta 180 (90 ) ⇒ 70 Si se considera a el cateto opuesto al ángulo , y b el cateto opuesto al ánguloIi) Hora y fecha de paso por dicho punto 95 Dos barcos A y B salen a las 05 00 horas del día 1 enero de un punto C (lat 30 ° 3 ′ 5 N , Long 1 ° O ) , a través de arcos de circunferencia máxima A navega con rumbo de salida N 60 ° E y con velocidad de 15 nudos , B navega con rumbo de salida N 30 ° O y con velocidad de 18
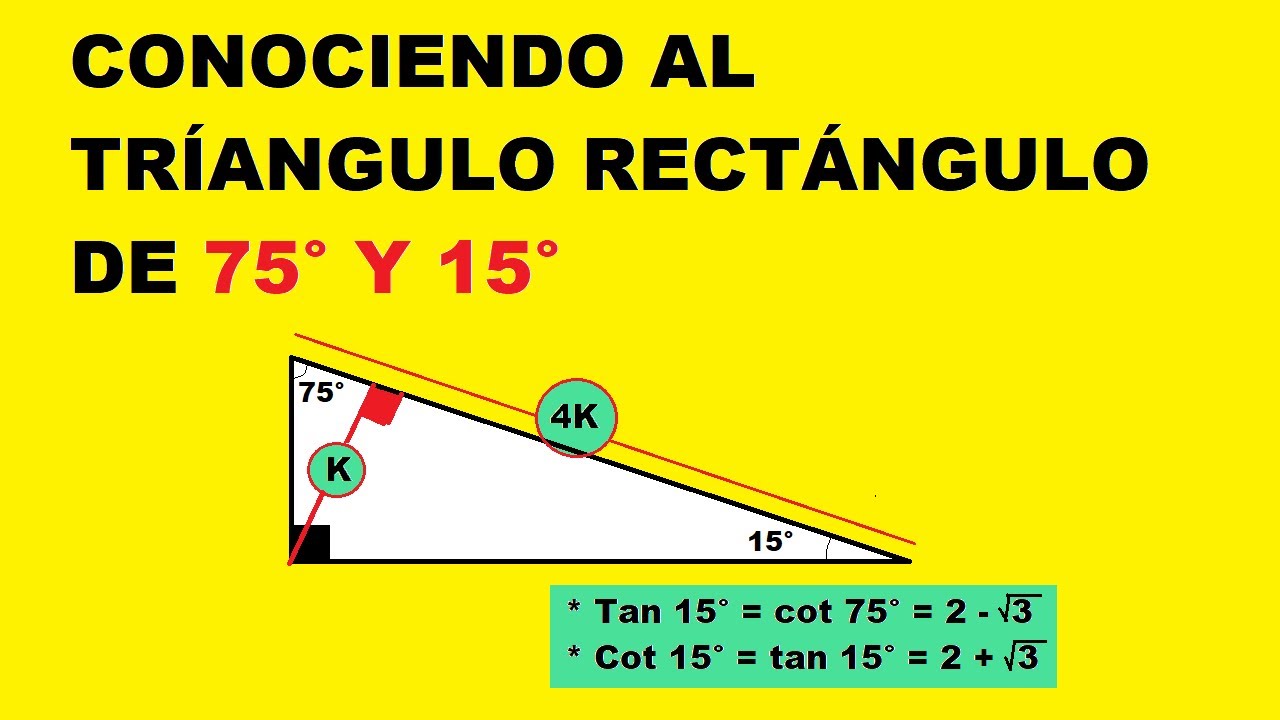



Un Interesante Triangulo Notable 75 Y 15 Conclusiones Youtube




57 Ideas De Razones Trigonometricas Razones Trigonometricas Trigonometria Calcular El Area
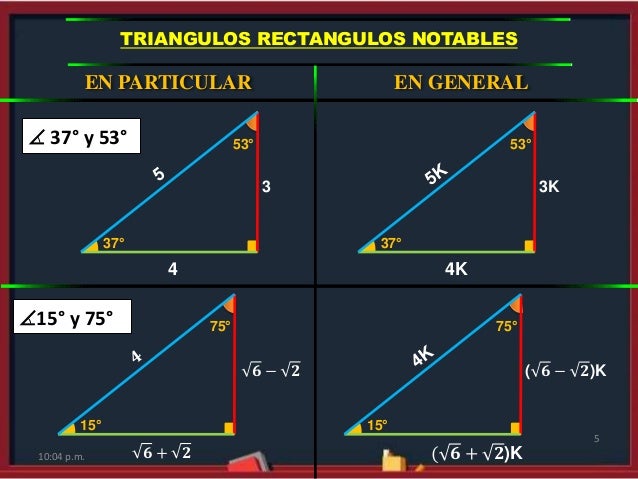
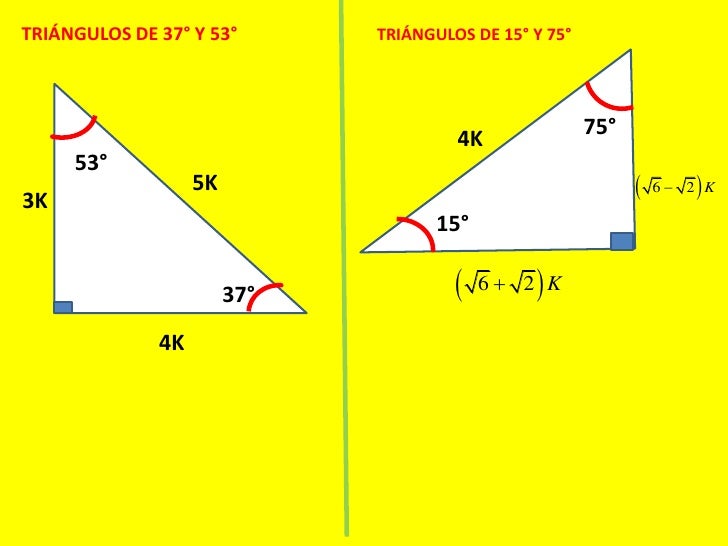
Otros triángulos notables no tan conocidos son El triángulo de 15 y 75 El triángulo de 18 y 72 El triángulo de 36 y 54 Relaciones metricas de un triangulo Relaciones Metricas de un triangulo Relacion Metrica Relacio metrica entre varios segmentos esTriángulo de 15° y 75° La altura relativa a la hipotenusa mide la cuarta parte de la longitud de dicha hipotenusa ° 1K K√50 8° 7K El triangulo de 8 y 30° K √3 74° 2K 25K 7K 60° 1K El triangulo de 30 y 60 16° 24K El triangulo de 16 y 74 8 √10K K 37°/2 3K El triangulo de 37/2 75° (√6 √2)K 4K √5 K K 15° (√6 √2)K El triangulo de 15 y 75 53°/2 2K El triangulo de 53/2 9




Triangulo Notable De 15º Y 75º Demostracion Youtube




Como Calcular Un Triangulo Equilatero 3 Pasos




Ejercicios Con Triangulos Oblicuangulos Superprof




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulo Rectangulo Notable De 15 Y 75 Youtube




Triangulos Notables Ejercicios Resueltos Pdf




Todo Los Triangulos Notables Sus Angulos Medidas



コンプリート 15 Y 75 Triangulo Notable 1067 Triangulo Rectangulo Notable De 15 Y 75 Josspix8pyh




Ficha Online De Semejanza De Triangulos




Triangulos Notables Ejercicios Resueltos Pdf




Que Datos Necesitas Para Encontrar La Medida Del Area De Un Triangulo Donde Esta Altura Brainly Lat




Triangulo Isosceles




Ficha 1 Teorema De Pitagoras




Triangulo Entero Wikipedia La Enciclopedia Libre




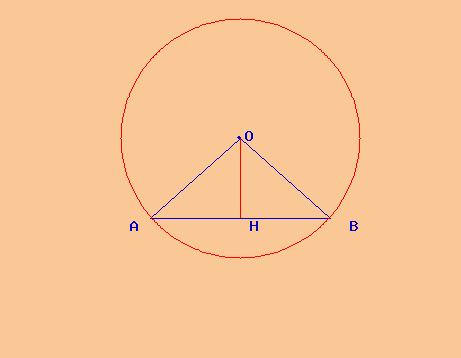
Cual Es La Altura H Del Triangulo Abc Necesito Ayuda Si Alguien Es Tan Amable De Explicar El Tema Brainly Lat




Triangulos Rectangulos Notables Matemath




Triangulos Rectangulos Notables Matemath



2




Problema 434




En Un Triangulo Isosceles La Base Mide 15 Y La Altura Relativa A Uno De Los Lados Congruentes Mide Brainly Lat




16 Ideas De Geometria Del Espacio En 21 Geometria Del Espacio Geometria Ejercicios Resueltos



Ejercicios De Escalas




Resolucion De Triangulos Pagina Pdf Descargar Libre




Triangulos Rectangulos Notables Matemath




Resolucion De Triangulos Superprof



コンプリート 15 Y 75 Triangulo Notable 1067 Triangulo Rectangulo Notable De 15 Y 75 Josspix8pyh




Razon Trigonometrica Tangente Worksheet




Como Calcular La Altura Del Techo De La Calculadora Como Calcular La Altura De La Cresta Del Techo Que Tipos De Estructuras De Techos Modernas Son Comunes




Magisterio De Bolivia Facebook




Altura De Un Triangulo




Triangulos Rectangulos Notables Matemath




Solucionador Automatico De Problemas De Geometria El Triangulo



Dreer Del Catalogo De Otono De 1910 1910 Catalogo De Otono 1910 De Dreer Dreers1910otono1910henr Ano 1910 Sklf Clfaning Automatico I Frames Sfegold Fl Gt Vl Lilujjg Hustler Cesped Rastrillo Pedestales De Planta Alambre Z Estante Cuadrada




Triangulos Notables Ejercicios Resueltos Pdf




Ejercicio Online Gratuito De Triangulos




Triangulos Rectangulos Notables Matemath




Trigonometria Resolucion De Triangulos Pdf Descargar Libre




Ejercicios Capitulo7 Geometria Plana



Manual De Construccion El Costo Y La Eficiencia Fig 294 Una Carpa O En Cuna Tamano Ft De Altura Ft 8 Oz Llenado Ducksingle 12 Oz Llenado Duckdouble 5x 77x 77x




Sem5 Proporcionalidad Y Semejanza Pdf Triangulo Geometria Elemental



En Un Triangulo Isosceles La Base Mide 15 M Y La Gauthmath




4 Resolver Triangulos




Triangulo Notable De 15 Y 75 Profesorajesus Com



Solucionador Automatico De Problemas De Geometria El Triangulo




Perimetro De Un Triangulo Rectangulo



Triangulos Notables




Triangulos Rectangulos Notables Matemath
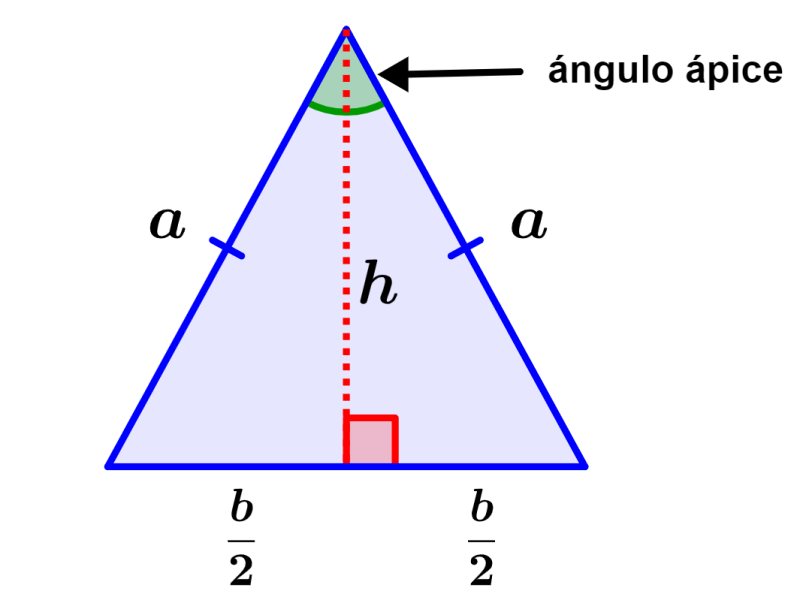



Caracteristicas Del Triangulo Isosceles Neurochispas




Ejercicios Con Triangulos Oblicuangulos Superprof




Descargar
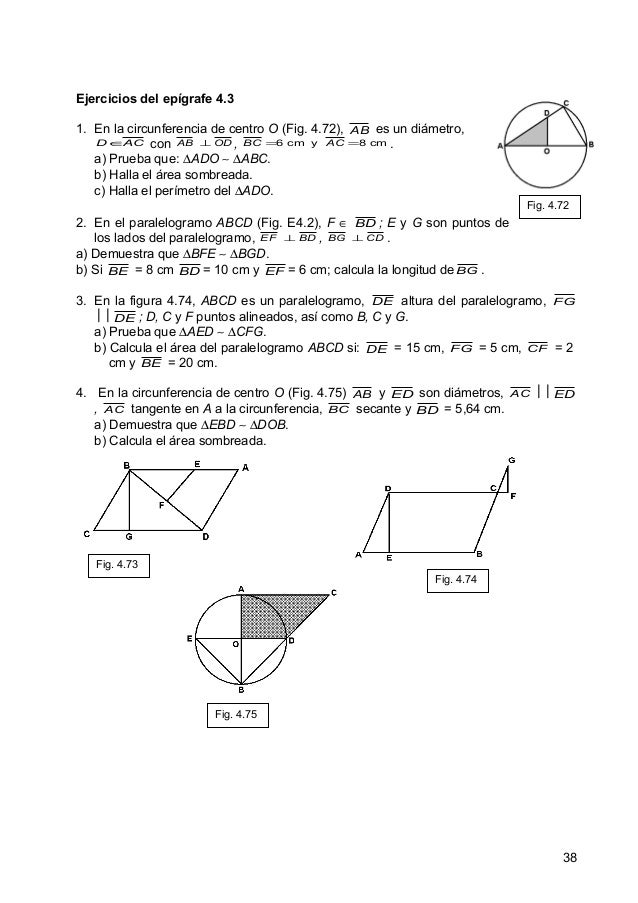



Capitulo 4 Pp 294 339 Word




Caracteristicas Del Triangulo Isosceles Neurochispas




Pagina 172 Pag 1 Unidad 8 Teorema De Pitagoras Semejanza Pdf Descargar Libre




4 Resolver Triangulos
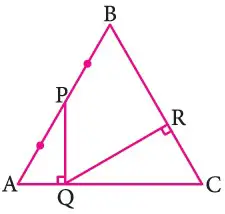



コンプリート 15 Y 75 Triangulo Notable 1067 Triangulo Rectangulo Notable De 15 Y 75 Josspix8pyh




Altura De Un Triangulo
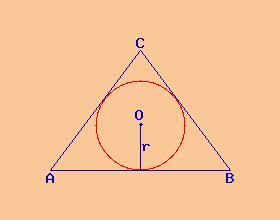



Solucionador Automatico De Problemas De Geometria El Triangulo




Resolucion De Triangulos Superprof



コンプリート 15 Y 75 Triangulo Notable 1067 Triangulo Rectangulo Notable De 15 Y 75 Josspix8pyh




Resolucion De Triangulos Superprof
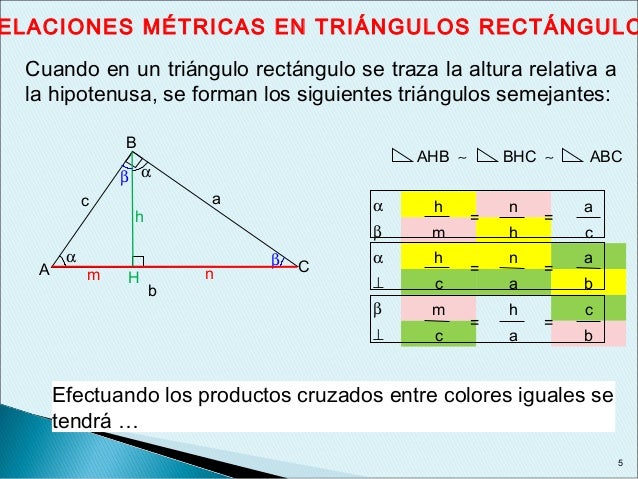



Relaciones Metricas En El Triangulo




Libro De Muestra Ilustrado Y Lista De Precios De Las Cartas De Transferencia De Patentes De Palm Ornamentos Y Disenos Comerciales Para Senales Vagones Coches Maquinas Etc Mejora La Modernidad Precio




Prueba Teoremas De Pitagoras Octavo 18
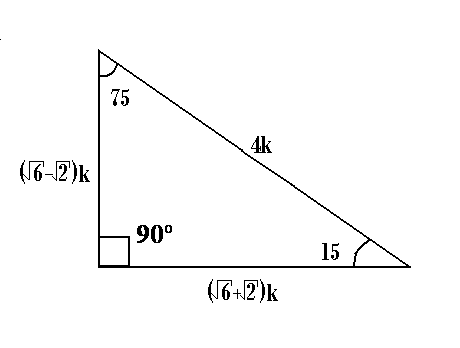



File Triangulo Auxiliar De 75 Y 15 Png Wikimedia Commons
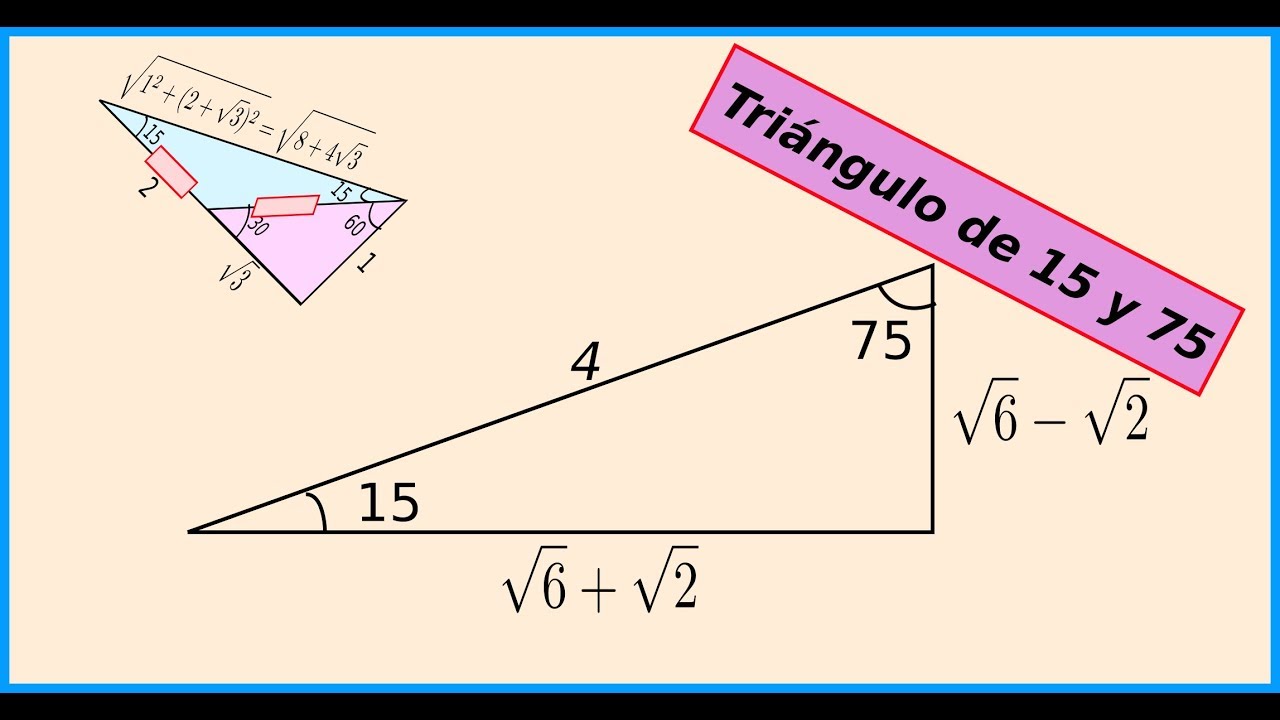



El Triangulo De 15 Y 75 Grados Youtube




Todo Los Triangulos Notables Sus Angulos Medidas




Soluciones Pag 235 Matematicas 3º Eso Docsity




Un Electricista Debe Colocar Un Armaje De Hierro Que Representa Un Arbol De Navidad De Forma Brainly Lat




Quiz Trigonometria1 Pdf
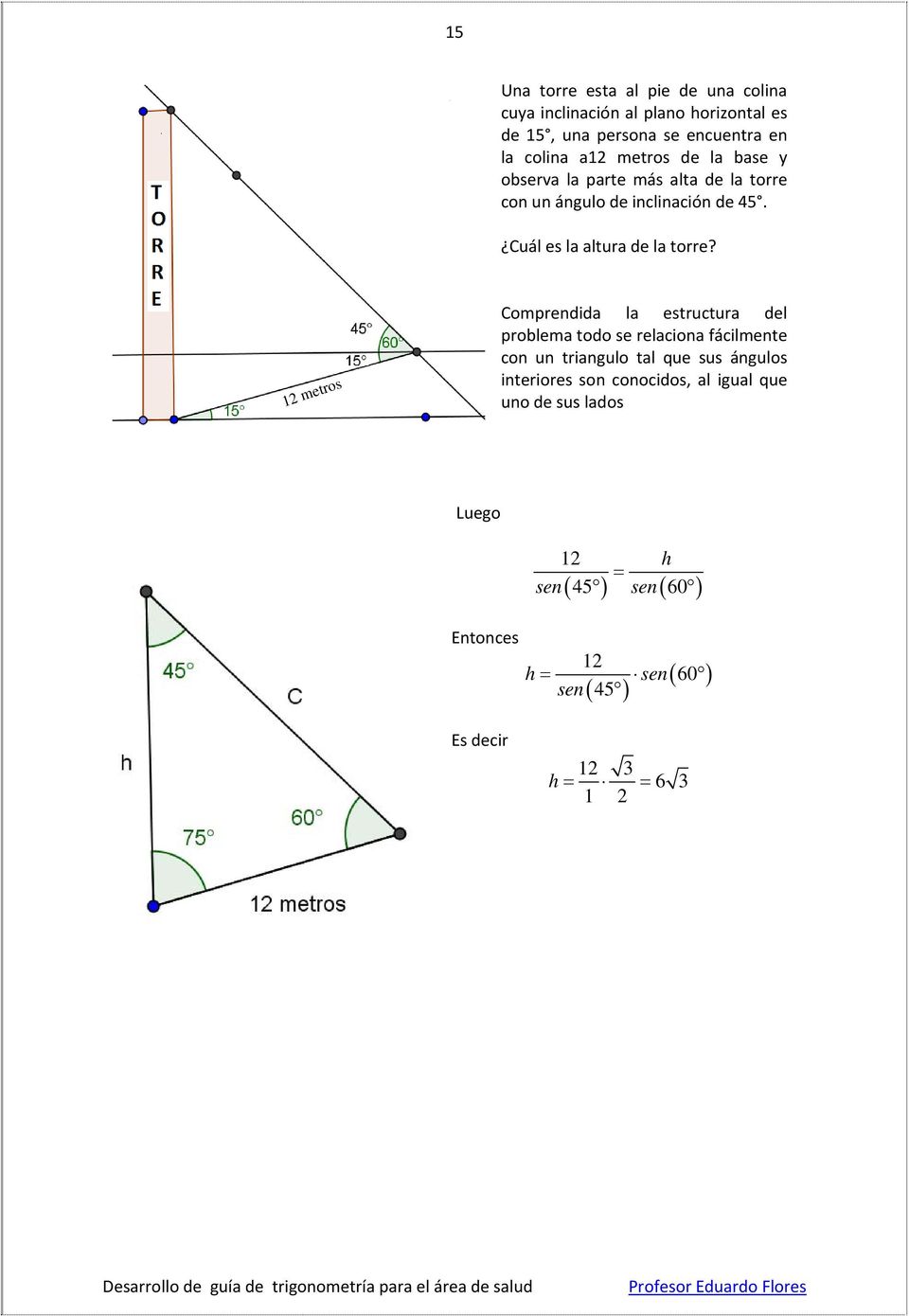



Los Catetos De Un Triangulo Rectangulo Miden 3 Cm Y 4 Cm Respectivamente Cuanto Mide El Coseno Del Menor Angulo 3 Sin A 5 4 Cos A Pdf Descargar Libre




Un Alma Por Otra Alma Pdf Formas Geometricas Triangulo



Marina En La Naturaleza Storyboard By C22ed67f




Grupo Uni Ingreso Seguro Added Grupo Uni Ingreso Seguro




Triangulo Isosceles
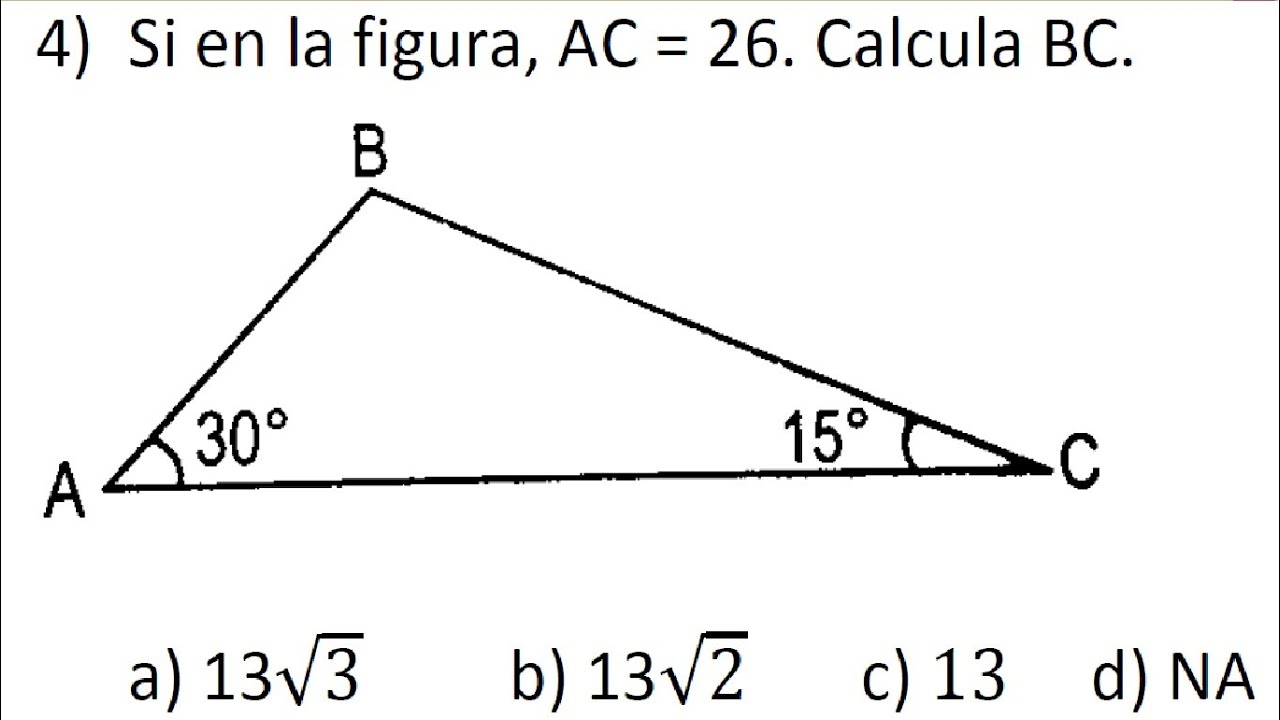



コンプリート 15 Y 75 Triangulo Notable 1067 Triangulo Rectangulo Notable De 15 Y 75 Josspix8pyh




Ejercicios Propuestos Pdf Descargar Libre



0 件のコメント:
コメントを投稿