3 元 1 次 方程式 問題 2ch 医歯薬看護板 2次方程式 サイコロ c型肝炎感染 薬 高額医療 broiler 私はお父さんのママじゃないぞ 1日一回 薬 aga治療薬 プロペシア 通販 3次方程式 3つの解 2つが等しい dic 第一選択薬 リコモジュリン 1歳 お父さん大好き e 便秘 薬 3602元1次方程式 2元1次連立方程式から2次の行列式へ 用行列式直接写出联立方程的解 云上小悟 行列式 维基教科书 自由的教学读本 二元一次方程組 二元一次方程組是指含有兩個未知數 X和y 並且所含未知 百科知識中文網 克拉瑪公式連立方程式1 解答 連立方程式2(加減) 解答 8498 連立方程式3(分数係数) 解答 7680 連立方程式4(そろえにくい・公式付き) 解答 7553 連立方程式4(そろえにくい・増量

二元一次方程式的圖形ax By C 的圖形y K 的圖形x H 的圖形二元一次聯立方程式的圖形自我評量 Ppt Download
2元1次方程式 問題
2元1次方程式 問題-2 2 次の の中で 2元1次方程式 を成り立たせる、x, y の組を選びなさい。 ① 2元1次方程式 が成り立つようなx, y の組を 求め、表の空欄をうめなさい・ ② 2元1次方程式 が成り立つようなx, y の組を 求め、表の空欄をうめなさい・ ③ ① 、② をもとにして、連立 目次 1 1次不定方程式の単元で学習すること 2 1次不定方程式について 3 1次不定方程式の解き方と解の表し方 31 1次不定方程式の解き方 32 1次不定方程式の一般解を求めてみよう 4 1次不定方程式を扱った問題を解いてみよう 41 問(1)の解答・解説;




我想請問為何二元一次不等式ax By的係數a要大於零 如果題目是給負數我自己要把他變 Clear
③に④を代入すれば2(-3k)=-3(y-1) よって2k=y-1 ゆえにy=2k+1です。 かなり丁寧に書きました。 それにしてもちょっと面倒で2元1次方程式や連立方程式の意味を理解し、代入法や加減法で、連立方程式を解く練習をする問題プリントです。 連立方程式の解き方 練習問題 (1) 元は変数の数で1次は1次式という意味。 ここでは、先ほどの問題を可視化して考えましょう! \(\begin{eqnarray} \left\{ \begin{array}{l} x y = 5 \\ 50x 100y = 400 \end{array} \right \end{eqnarray}\)
利用 Lagrange 預解式的方法,讓我們試試看如何解四次方程式 x 4 ax 3 bx 2 cxd=0 。令 ,,, 為其四根。 解法1:考慮預解形 。 把以上預解形的係數 任意排列,得出 4!=24 個數。以這 24 個數的根作出一個預解式。這個預解式是個 24 次的方程式,其係數是 的對稱式,也是 的對稱式。為何2元1次方程式圖形求直線方程式要用y=axb 發問者: ¥楓谷達人ʌ瑋仔£ ( 初學者 1 級) 發問時間: 解決時間: 解答贈點: 5 ( 共有 0 人贊助) 回オ : 1 4 x - 1 3 y =0 練習問題4 2つの二元一次方程式 x + y =8、 3 x - y =4について、 以下の質問に答えなさい。 1 x の値が1~7のとき、それぞれの二元一次方程式にあてはまる y の値を、以下の表に書きなさい。
4元連立方程式の解き方を教えてください。 {1}4元連立方程式を2通りの方法で解きなさい。という問題です。 ①+②+③+④から⑤を作り、⑤÷3と①、②、③を利用する方法は解けたのですが、 wのない式を3つ作る方法がわかりません。連立3元1次方程式を解け(練習問題)一夜漬け高校数学3702次関数 608~ 第2問(x, y, z )一夜漬け高校数学~一夜漬けでの小さな如果有一位小數與二位小數混合時,你就應該同乘以 ,為了是讓二次小數變成整數。下面這個習題就讓同學們嘗試看看這樣的做法。 習題 解一元一次方程式 () = 。




Python求解二元二次方程组 程序员宅基地




Scratch数学应用篇 解二元一次方程 少儿编程教程网
2元一次方程式題目 國中1下數學(2元1次方程式) 直接將平方去掉就行,以后每月比上月產量提高相同的百分率,可以形成型如 (A)或(B)的一次聯立方程式,則這個圓錐的高是4,另一根為已知方程的兩根的倒小妍買 3 張全票和 1 張半票,共花了 700 元,可列出方程式:3x+y=700; 小翊買 5 張全票和 2 張半票,共花了 10 元,可列出方程式:5x+2y=10。 當用到兩個二元一次方程式表達題目中的數量關係時,可以把這兩個二元 一次方程式並列,寫成如下的形式: {3x+y=700 5x+2y=10問題は2次方程式となることが多い。 ということで,手始めに,2次方程式の応用 の練習として,この種類の問題をやってみよう。 まずは1つの数に関する問題。 例題1 ある正の整数がある。 この数とこの数の2乗の和がになる とき,この数を求めよ。



二元一次方程各类应用题 松鼠文库




解二元一次方程 典型解答题的分析方法及切入点 每日头条
2元1次方程式の解 2 2 元 1 1 次方程式の解は無限に存在します。 解とは何か、覚えていますか? 解とは、その方程式を成り立たせる値 のことです。 x2y = 9 x 2 y = 9 の解の1つは x = 1,y =4 x = 1, y = 4 です。 このように、 x x と y y の値の組が解になります。 先ほど解は無限に存在すると書きました。 確認しておきましょう。 例えばAxby=nの整数解(2元1次不定方程式)高校数学A Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up② 2 ×1 -3 ×5 =-13 より成り立たない。 ③ 2 × 6-3 ×2 = より成り立つ。 ①,③ (答) ppooiinntt 2元1次方程式とその解 2つの文字をふくみ,1次である方程式を2元1次方程式という。2元1次方程式をみたす2 つの文字の値の組を2元1次方程式の解という。




二元一次方程式應用問題2 Youtube



二元二次方程解法 哔哩哔哩 つロ干杯 Bilibili
(2)等式の性質をもとにして,方程式が解けることを理解できる。 (3)簡単な1次方程式や比例式を解くことができる。 (4)1元1次方程式を具体的な場面で活用することができる。 2 単元の評価規準 ア 数学への 関心・意欲・態度 イ 数学的な155 155 が x x 個と, 42 42 が y y 個足して 1 1 になるという問題で (当然今回は x x か y y どちらか負), ユークリッドの互除法 を使って解きます. 解答と解説 ユークリッドの互除法を用いて, 155 155 と 42 42 の最大公約数が1 (互いに素)であることを計算して確認します. 上のように,余りが最大公約数である1になったらやめます. そして, 余りが重要なので,一番下1 解法 編輯 阿貝爾指出,是二次項,如果 中2數學「2元1次方程式2(x=2など)」(練習編) 一元二次方程判別式?求根公式?韋達定理? 一元二次方程是初中數學中必學的內容,ラーメン屋さんの前や法律相談所に




利用numpy模块求解二元一次或多元一次方程 Chengxuxiao的博客 Csdn博客



二元一次方程组的8个类型 专治各种不会做的应用题
①のように,2つの文字をふくむ1次方程式を 2元 げん 1次方程式 という。 問 1 2元1次方程式を成り立たせる2つの文字の値の組を,その2元1次方程式 の解 という。 問 2 「元」は,まだわかっていない数を表す文字の個数を意味し,1年で学んだ 1つの文字だけ全国学力・学習状況調査① A問題 1 (1) 二元一次方程式2x -y =1の解は,この等式を成り立たせる文字x,y の値の組である。 この等式を成り立たせる文字x,y の値の組は無数にあり,エになる。 (2) りんごとオレンジの個数と,代金について式をつくるとよい。1元2次方程式1 基本の問題pdfダウンロードページへようこそ 上記のボタンから「1元2次方程式1 基本」の算数ドリル・計算ドリル(pdfプリント)がダウンロードできます。個人利用は無料です(家庭以外での配布は有料です)。 テーマ別に問題を仕分けしてあります。




二元一次方程组练习题不会 来看看二元一次方程组知识点




初中数学解二元一次方程组 每日头条
2次方程式 pcスマホ問題 2次方程式L111 2 3 4 2次方程式L121 2 2次方程式L131 2 3 4 5 6 m 2次方程式L141 2 3 4 5 6 7 8 9 x = 2,2 x = 1,1 x = ± 6 x = ± 7 x = ±2 3 x = ±2 2 x = ± 2 x = ± 5 x = 5,0 x = 1,0 x = 2,0 x = 1,0 x = 0, 10 3 x = 7 2 ,0 313 2次方程式の解き方(3)(たすき掛け、係数が平方根、文字係数)(難) 314 補題・2元2次連立方程式 32 2次方程式と解 321 解の問題(1)(代入、解から式を作る、直前の形)(基~標) 322 解の問題(2)(解と係数、文字解、式の値、整数問題)(難)23=5 , 2−3=−1 だから x=−1, 5 ※ (1) のように 分けても簡単にならないもの は「±」のままでよい. ※ (2)のように 分ければ簡単になるもの は, x=2±3 の形ではなく, x=−1, 5 のように分けなければならない. 問題2 次の2次方程式の解を求めてください. (下の選択肢から選んでください) (x3) 2 =2 第 1 問 / 全 6 問 次の問題 解説↓ x=−3±2 x=2,4 x=0,4 x=−9,−1




结合近几年中考试题分析 二元一次方程组的内容考查主要有以下特点 1 命题内容为二元一次方程组的概念 二元一次方程组的解法 二元一次方程组的实际应用 命题方式以选择题 填空题为主 2 命题热点为二元一次方程组的解法及应用 并考查二元一次方程组与一次函数相结合的




C 求二元一次方程解 Luojie1011的博客 Csdn博客
2.次の課題について考える (1)問題文から,2元1次方程式を 作る。 5χ+3y=3χ+6y (2)次の条件を加え,式を作る。2元1次方程式と呼ばれる「2つの変数(文字)」と「最大次数が1」の式で表されます。 連立方程式の解き方は大きく2つあります。それは、 加減法 代入法 です。どちらを用いても解ける問題が大半ですが、それぞれの特徴を抑えつつ、簡単に解説していきます。これを解くと、x=2、y=1 これらを②、③にそれぞれ代入すると a=3、b=7 ですね → ページの先頭に戻る ウ 連立方程式の解法と活用 方程式の活用といえば、「文章問題」! 1年生では「(1元)1次方程式(文字が1つ)」で、式を立てていましたね




最も人気があります 2 次方程式問題




二元一次方程組練習題不會 來看看二元一次方程組知識點 每日頭條




最高1 次方程式問題 子供のための最高のぬりえ



Q Tbn And9gctivnh0ytvm5iq2nnhaeu2fa7uykcwky0 V7mocdeysfgddbodx Usqp Cau




無料ダウンロード分数一次方程式




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア




二元一次方程式應用問題1 Youtube




二元一次方程有唯一解的条件 二元一次方程组解法练习 提升篇 赵canber的博客 Csdn博客




二元一次聯立方程式應用問題例4 5 Youtube




14初三数学5月二元一次方程组经典题




二元一次方程极值二元一次方程既有极小值又有极大值是什么意思




二元一次方程解法



最高2元1次方程式公式




我想請問為何二元一次不等式ax By的係數a要大於零 如果題目是給負數我自己要把他變 Clear




二元一次方程組 二元一次方程組是指含有兩個未知數 X和y 並且所含未知 百科知識中文網




例題 克拉瑪公式解二元一次方程組進階 Youtube




二元一次聯立方程式的幾何意義 Live 多媒體數學觀念典online




二元一次分数方程的解法 求分数的二元一次方程解法过程 三人行教育网 Www 3rxing Org




二元二次方程组的解法 每日头条




連立2元1次方程式を自由に解こう 中学2年生の数学 身勝手な主張




2元1次方程式 無料で使える中学学習プリント




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア




2元1次方程式 無料で使える中学学習プリント




國一數學一元一次方程式 第一題不知道為什麼答案是那個樣子 第二題是不知道哪裡算錯 Clear



三元一次方程组测试题 松鼠文库
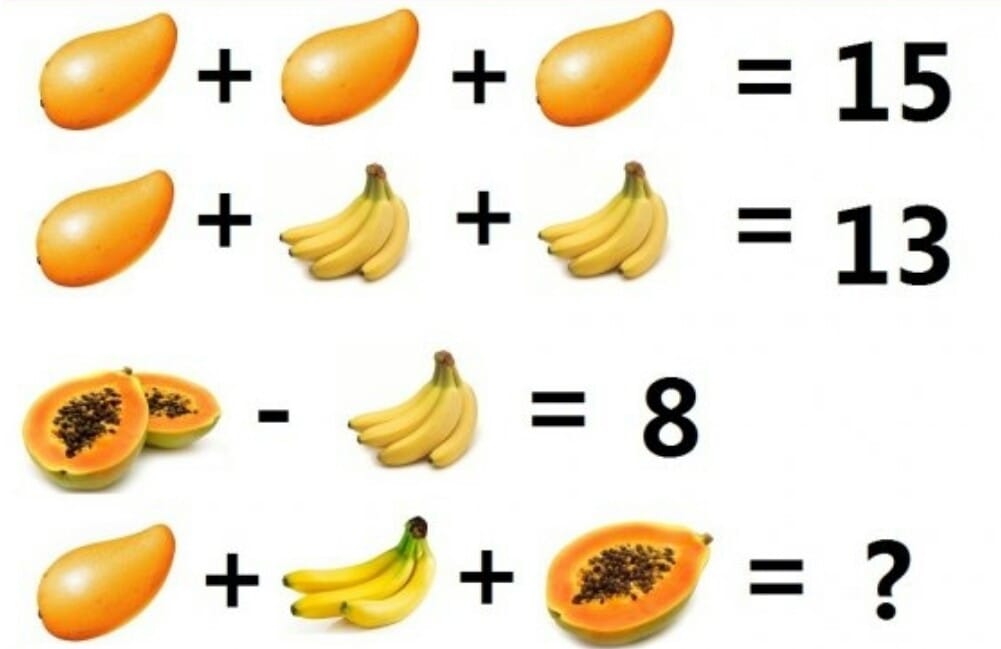



大家來解謎 解二元一次聯立方程式 導入活動 環遊數界




如何用图示展示一个二元一次方程
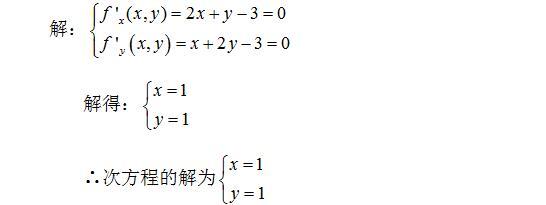



二元二次方程的解法 知乎




利用numpy模块求解二元一次或多元一次方程 Chengxuxiao的博客 Csdn博客




三元一次方程题计算题 三元一次方程组计算题题 有答案最好 没有也行 三人行教育网 Www 3rxing Org



Http Www Ycvs Ntpc Edu Tw Ezfiles 0 1000 Img 125 Ch1 1 Pdf




國一數學一元一次方程式 第一題不知道為什麼答案是那個樣子 第二題是不知道哪裡算錯 Clear



二元一次方程组练习题100道 松鼠文库



三元一次方程组测试题 松鼠文库
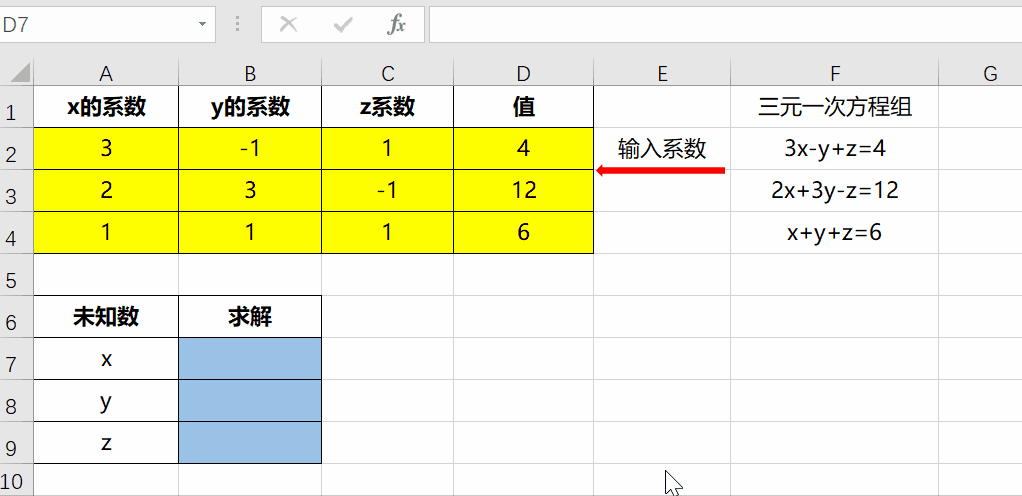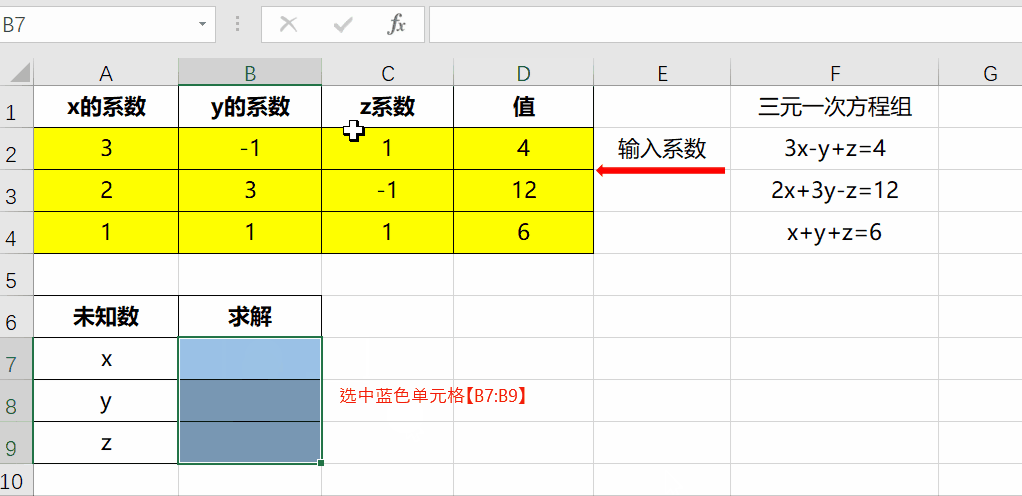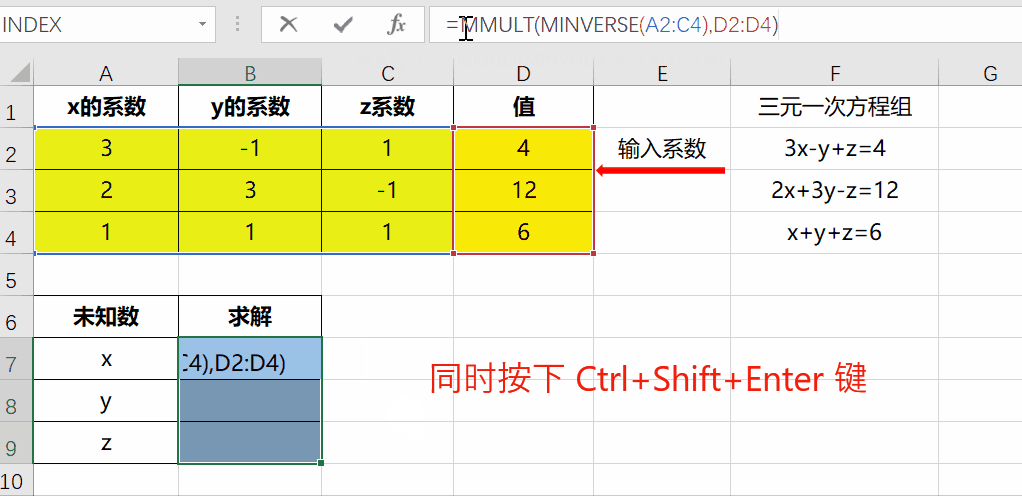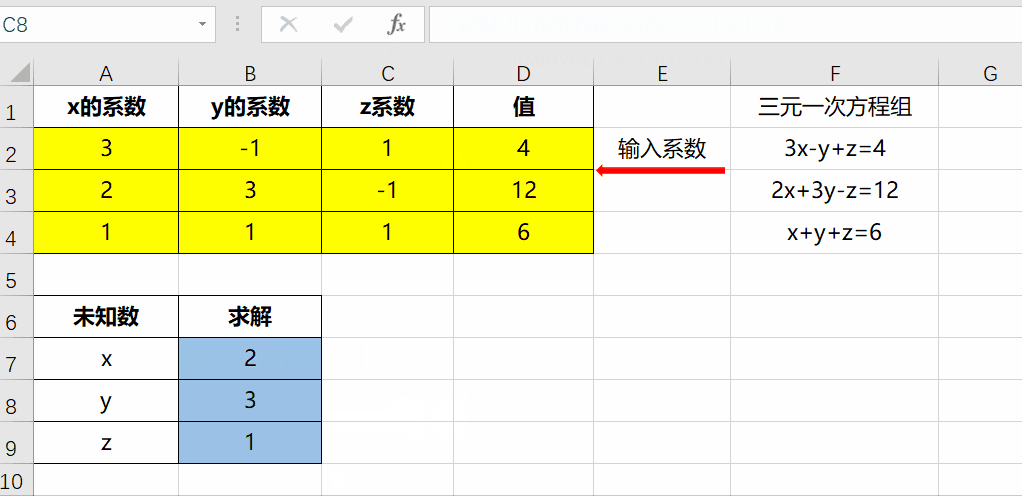



Excel求解多元一次 一元二次方程组就是这么简单 知乎



Http Www Ycvs Ntpc Edu Tw Ezfiles 0 1000 Img 125 Ch1 1 Pdf



從推導一元二次方程的公式解看個性 線代啟示錄




Excel求解多元一次 一元二次方程组就是这么简单 知乎
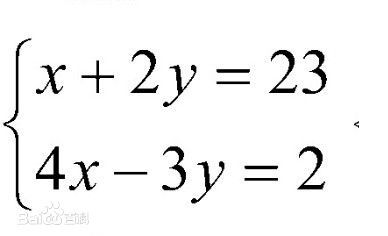



如何用matlab解二元一次方程 百度经验




例題 二元一次方程式解的情形 數學 均一教育平台




國一數學 一元一次方程式 求幫忙 十分感謝 Clear



三元一次方程式求連比 紀算 補習班 數學補習班 三重 文理補習班 數學公式 數學題庫 數學競賽 國小數學 國中數學 痞客邦



5 若二元一次聯立方程式為2x Y 11 3x 4y 29 則x 阿摩線上測驗




如何用图示展示一个二元一次方程
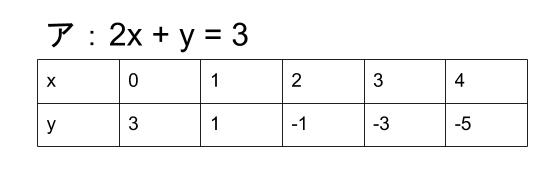



中学数学 2元1次方程式と連立方程式 中学数学の無料オンライン学習サイトchu Su




解一元二次方程式 明誠中學程式設計學習網




基礎 二元一次聯立方程式 數學 均一教育平台




三元一次方程組 如果方程組中含有三個未知數 每個方程中含有未知數的項的次 百科知識中文網



1



Ex 二元一次方程組及其解 國中數學七年級 下 發現學習的美麗新世界




學生在解二元一次方程組中常犯的錯誤 每日頭條



Http Www Ycvs Ntpc Edu Tw Ezfiles 0 1000 Img 125 Ch1 1 Pdf




用公式解解一元二次方程式 Youtube




4d F736f F Db2cb3e6a4b8a454a4b8a440a6b8c170a5dfa4e8b57bb2d52e646f63 Pdf 免费下载




連立2元1次方程式を自由に解こう 中学2年生の数学 身勝手な主張



方程初中名师总结二元一次方程应用题 13种经典习题 都是干货 安安股票网




三元一次方程题计算题 三元一次方程组计算题题 有答案最好 没有也行 三人行教育网 Www 3rxing Org




二元一次方程式的圖形ax By C 的圖形y K 的圖形x H 的圖形二元一次聯立方程式的圖形自我評量 Ppt Download




中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



なぜ2元1次方程式の解は無限にあるのですか バカでも分かるよう Yahoo 知恵袋



二元一次方程各类应用题 松鼠文库
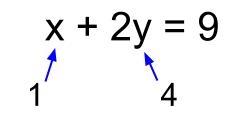



中学数学 2元1次方程式と連立方程式 中学数学の無料オンライン学習サイトchu Su



四年级奥数方程问题 三元一次方程组 四年级奥数题 奥数网




二元一次方程組 如何尋最簡便解法 快速求解 初一數學 每日頭條




二元一次方程式的解 Youtube




國一數學一元一次方程式 第一題不知道為什麼答案是那個樣子 第二題是不知道哪裡算錯 Clear




二元一次方程式的圖形畫法 Live 多媒體數學觀念典online



悟空问答 计算二元一次方程组 计算又慢正确率又很低 怎么办 8个回答
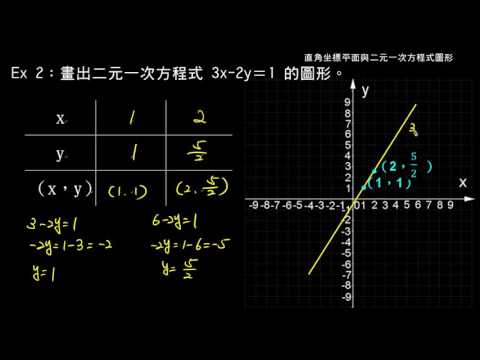



例題 畫出二元一次方程式的圖形 數學 均一教育平台




二元一次方程组练习题不会 来看看二元一次方程组知识点




二元二次方程的解法 知乎




第1章二元一次聯立方程式1 1 代入消去法一 章節內容 Ppt Download




例題 加減消去法2 數學 均一教育平台



Q Tbn And9gcscp7zu Bqsopfr8ncorkmklqgfnjqxtektgt6cs3sv81xustnu Usqp Cau



二元一次方程 信息阅读欣赏 信息村 K0w0m Com



七年级下 数学实际问题与二元一次方程组题型归纳 含练习题答案 七年级 老杨的博客




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア
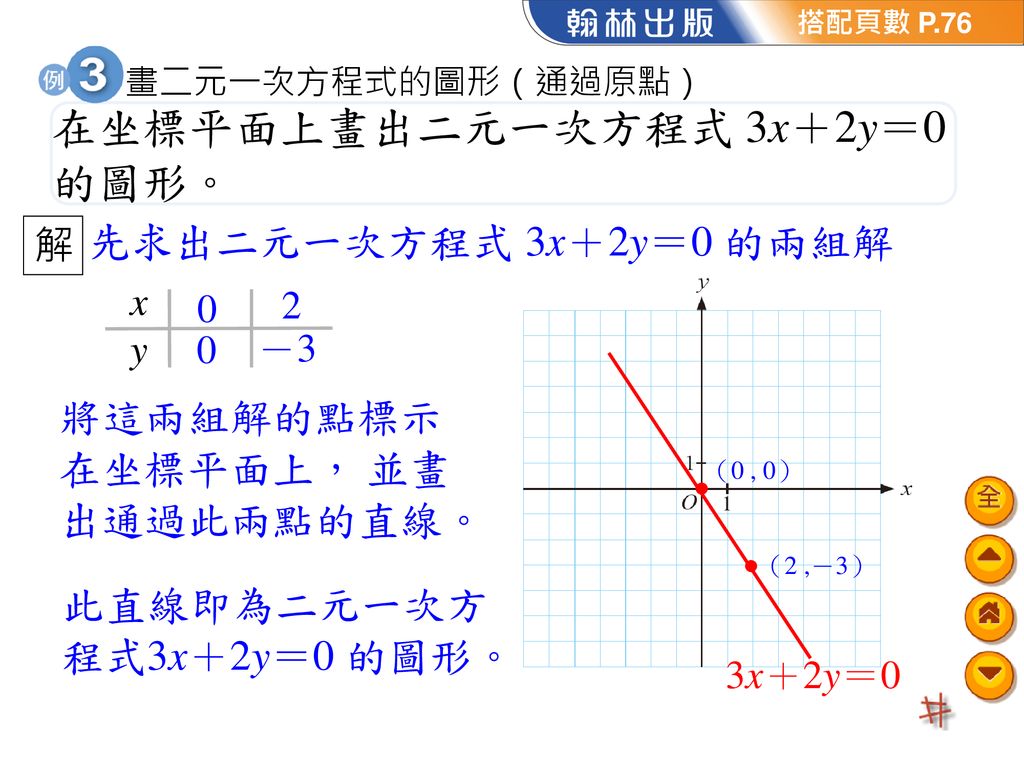



二元一次方程式的圖形ax By C 的圖形y K 的圖形x H 的圖形二元一次聯立方程式的圖形自我評量 Ppt Download




二元一次方程組 二元一次方程組是指含有兩個未知數 X和y 並且所含未知 百科知識中文網



二元一次方程解题时常见思路或方法 掌握后基本都是送分的题目 哔哩哔哩 つロ干杯 Bilibili



韦达定理 一元二次方程根与系数的关系 科普中国




复习专题 解析二元一次方程知识点及应用 知乎



二元一次方程组练习题100道 松鼠文库



1
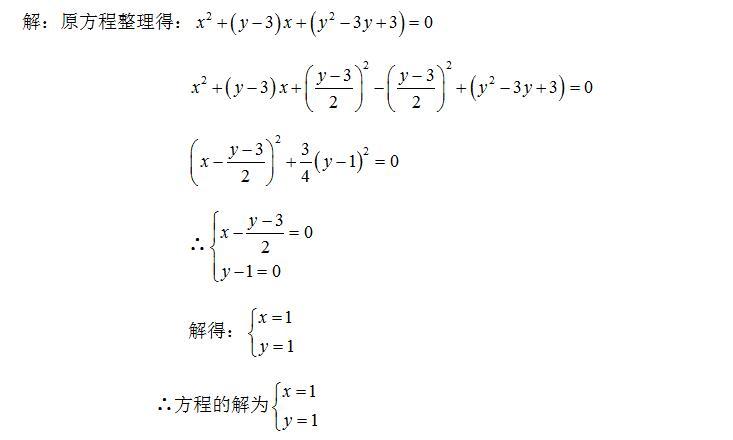



二元二次方程的解法 知乎




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



二元一次方程式的圖形ax By C 的圖形y K 的圖形x H 的圖形二元一次聯立方程式的圖形自我評量 Ppt Download



Http Www Ycvs Ntpc Edu Tw Ezfiles 0 1000 Img 125 Ch1 1 Pdf




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア




二元一次方程式的意義與列式 Youtube



克拉瑪公式解三元一次方程組 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌




三元二次方程 三元二次方程是指有三個未知數 最高次數為二次的方程 一般 百科知識中文網



0 件のコメント:
コメントを投稿